

 Nawigacja okruszkowa
Nawigacja okruszkowa
Nawigacja okruszkowa
Nawigacja okruszkowa
 Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
Widok zawartości stron

 Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
Interaktywna animacja b-drzewa (dr hab. Paweł F. Góra, prof. UJ)
Praca licencjacka z informatyki
Celem pracy jest wizualizacja działania b-drzewa: wstawiania, wyszukiwania, usuwania i modyfikacji elementów b-drzewa, wraz z równoważeniem b-drzewa. Użytkownik podaje parametry b-drzewa i zestaw elementów do utworzenia b-drzewa (lub może skorzystać z predefiniowanych zestawów, lub może wygenerować nowy zestaw), a dla już utworzonego b-drzewa element wyszukiwany, usuwany, modyfikowany lub pojedynczy element do wstawienia. Animacje muszą być zgodne z faktycznym działaniem algorytmów.
Symulacja ataku bizantyńskiego na sieć rozprzestrzeniania opinii (dr hab. Paweł F. Góra, prof. UJ)
Praca licencjacka z fizyki lub informatyki
W systemach rozprzestrzeniania się opinii rozpatrujemy "agentów" umieszczonych na siatce (grafie). Każdy "agent" ma opinię w pewnej sprawie, przybierającą wartość $\pm 1$.
Jeżli opinia większości zgadza się z opinią danego "agenta", nic się nie dzieje. W przeciwnym razie "agent" może przyjąć opinię większości z prawdopodobieństwem Boltzmannowskim.
Wśród "agentów" znajdują się zdrajcy, którzy, jeśli ich zapytać, zawsze kłamią - odpowiadają inaczej, niż aktualna wartość opinii pytającego (problem bizantyńskich generałów).
Pytania: Jak dynamika opinii, w tym ewentualne pojawienie się przejścia fazowego (jedna opinia dominuje), zależy od
Agregacja ograniczana dyfuzyjnie dla szumów kolorowych (dr hab. Paweł F. Góra, prof. UJ)
Praca licencjacka z informatyki lub fizyki
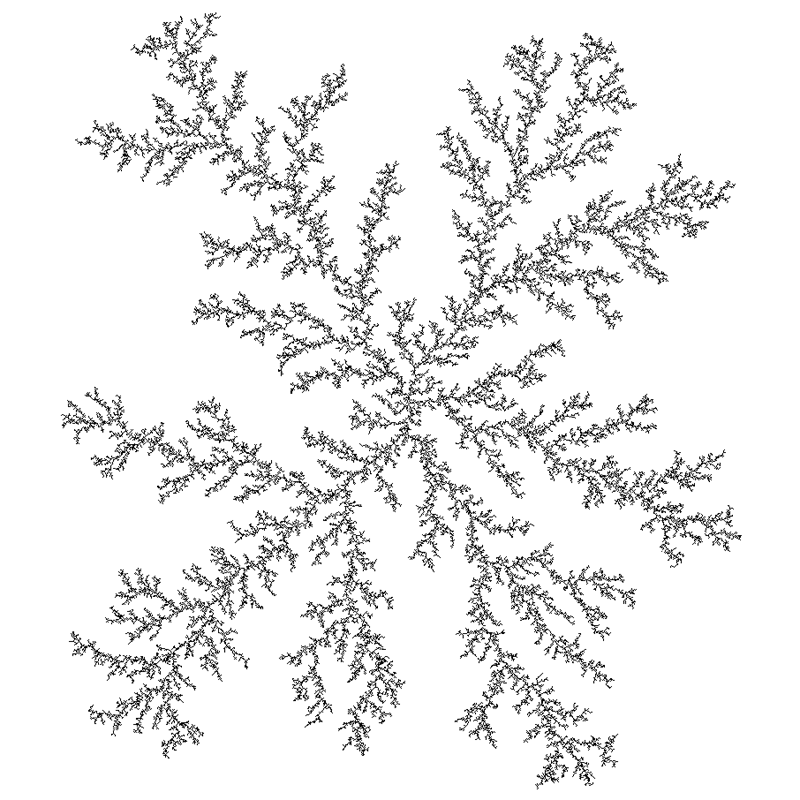
Agregacja ograniczana dyfuzyjnie (Diffusion Limited Aggregation) to proces, w którym błądzące przypadkowo cząstki przyklejają się do istniejącego klastra. Powstają struktury fraktalne. Celem pracy jest sprawdzenie, jak wymiar tych struktur zmienia się wraz ze zmianą parametrów opisujących pamięć (korelacje czasowe) szumu. Praca wymaga intensywnych, chociaż prostych, symulacji numerycznych.
Implementacja algorytmu Bulirscha-Stoera z ekstrapolacją Floatera-Hormana (dr hab. Paweł F. Góra, prof. UJ)
Praca licencjacka lub magisterska z informatyki dla desperatów
Algorytm Bulirscha-Stoera pozwala na znajdywanie bardzo dokładnych rozwiązań równań różniczkowych zwyczajnych przez ekstrapolację kroku całkowania do zera. Klasyczny algorytm oparty jest na ekstrapolacji wielomianowej. Celem pracy jest zastąpienie ekstrapolacji wielomianowej ekstrapolacją funkcjami wymiernymi, zgodnie z algorytmem Floatera-Hormana. Wymagane są intensywne obliczenia numeryczne.
Badanie własności upakowań losowych (dr hab. Michał Cieśla, prof. UJ)
Wszystkie poniższe tematy dotyczą badania losowych upakowań generowanych w następujący sposób,
Proces powtarzamy iteracyjnie. Upakowaniem nasyconym nazywamy takie, do którego nie da się dodać kolejnego obiektu. Podstawowym parametrem określającym losowe upakowanie jest jego gęstość (średnia liczba obiektów * objętość obiektu / objętość upakowania)
Wymiar fraktalny struktur w odwróconym procesie DLA (dr hab. Paweł F. Góra, prof. UJ)
Praca magisterska z fizyki lub informatyki
Cząstka, startująca z pewnego punktu początkowego, wykonuje błądzenie przypadkowe aż dotknie brzegu pewnej figury; początkowo figurą tą jest trójkąt równoboczny lub kwadrat. Gdy błądząca cząstka dotknie brzegu figury, ten "wybrzusza" się, tworząc trójkąt, którego podstawą jest dotychczasowy bok, a wysokość jest proporcjonalna do długości tego boku.
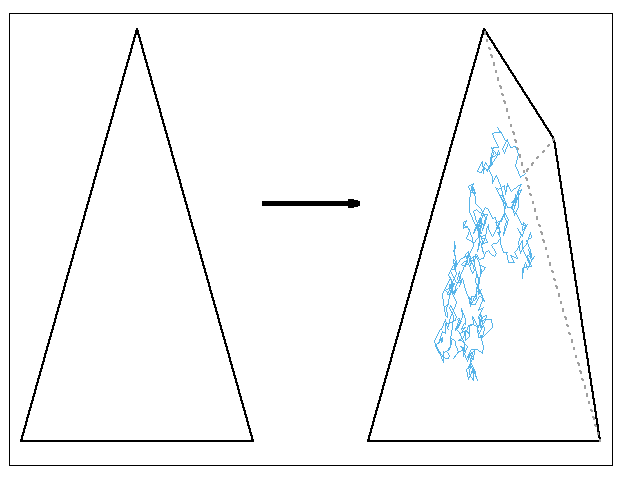 Cząstka wraca do swojego położenia początkowego i cały proces zaczyna się od nowa (ale figura ograniczająca obszar dyfuzji jest już zmieniona). Proces ten można traktować jako odwrócony proces agregacji ograniczanej dyfuzyjnie (Diffusion Limited Aggregation, DLA). Hipoteza: Po wielu iteracjach brzeg figury staje się fraktalny. Należy to potwierdzić i obliczyć wymiar fraktalny brzegu.
Cząstka wraca do swojego położenia początkowego i cały proces zaczyna się od nowa (ale figura ograniczająca obszar dyfuzji jest już zmieniona). Proces ten można traktować jako odwrócony proces agregacji ograniczanej dyfuzyjnie (Diffusion Limited Aggregation, DLA). Hipoteza: Po wielu iteracjach brzeg figury staje się fraktalny. Należy to potwierdzić i obliczyć wymiar fraktalny brzegu.
Praca może okazać się obliczeniowo znacznie bardziej skomplikowana, niż to się na pierwszy rzut oka wydaje. W przypadku sukcesu, możliwa będzie kontynuacja współpracy w innej formie.
Lwy i antylopy: Dynamika w modelu Kuramoto z dwoma antagonistycznymi gatunkami (dr hab. Paweł F. Góra, prof. UJ)
Praca magisterska z fizyki, biofizyki lub informatyki
Uogólnienie klasycznego modelu synchronizacji na przypadek gatunków antagonistycznych. Temat wydaje się koncepcyjnie prosty, ale może wymagać intensywnych obliczeń numerycznych.
Rezonans stochastyczny i rezonans koherencyjny w monostabilnych studniach potencjału (dr hab. Paweł F. Góra, prof. UJ)
Praca magisterska z fizyki
Uogólnienie wyników pracy Stationary distributions of a noisy logistic process, Acta Phys. Pol. B 36, 1981 (2005), na przypadek potencjałów $x^{2n}$. Możliwa kotynuacja współpracy.
 Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
Zapraszamy studentów zainteresowanych:
Teorią, układami złożonymi, sieciami…
Biofizyką, fizyką materii miękkiej…
Symulacjami, fizyką komputerową…
i nie tylko!
 Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
Widok zawartości stron
I Pracownia fizyczna MS / Sylabus
(K. Oleś)
I Pracownia fizyczna MT (cz.2) / Sylabus
(K. Oleś)
Język Java / Sylabus
(M. Cieśla)
Logika i teoria mnogości / Sylabus
(K. Oleś)
Matematyka I / Sylabus
(P. F. Góra)
Matematyka wyższa I / Sylabus
(K. Oleś)
Mechanika klasyczna MT / Sylabus
(B. Dybiec)
Metody numeryczne / Sylabus
(P. F. Góra)
Podstawy fizyki: Mechanika MT / Sylabus
(B. Dybiec)
Rachunek prawdopodobieństwa i statystyka / Sylabus
(B. Dybiec)
Seminarium doktoranckie z teorii układów złożonych – Mark Kac Seminar "Enigmas of Chance" / Sylabus
(E. Gudowska-Nowak)
Seminarium spec. I (fiz. teoret.) / Sylabus
(L. Longa)
Wstęp do programowania / Sylabus
(M. Cieśla)